前言
点积也叫內积，在我们的高中数学里叫做向量的数量积。f2i易塔云建站-模板下载,web开发资源,技术博客
点积是两个向量的相乘，其返回值是一个数字，而不是向量。f2i易塔云建站-模板下载,web开发资源,技术博客
使用点积可以计算力做的功、平面的受光强度、一个点位是否在三角形中等。f2i易塔云建站-模板下载,web开发资源,技术博客
我们之前说过，向量可以用坐标点位表示，也可以用方向和长度表示。f2i易塔云建站-模板下载,web开发资源,技术博客
所以点积的求值方式也有两种：f2i易塔云建站-模板下载,web开发资源,技术博客
- 基于向量的长度和夹角求点积
- 基于向量的坐标点求点积
接下来咱们就详细说一下这两个求点积的方式。f2i易塔云建站-模板下载,web开发资源,技术博客
f2i易塔云建站-模板下载,web开发资源,技术博客
f2i易塔云建站-模板下载,web开发资源,技术博客
第一章 基于向量的长度和夹角求点积f2i易塔云建站-模板下载,web开发资源,技术博客
f2i易塔云建站-模板下载,web开发资源,技术博客
1-基本公式
f2i易塔云建站-模板下载,web开发资源,技术博客
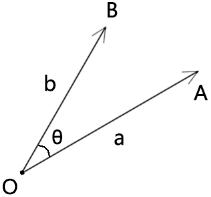
已知：f2i易塔云建站-模板下载,web开发资源,技术博客
- 向量a的长度是|a|
- 向量b的长度是|b|
- 向量a和向量b的夹角是θ
则向量a和向量b的点积为：f2i易塔云建站-模板下载,web开发资源,技术博客
a·b=|a|*|b|*cosθ
上面的公式就是基于向量的长度和夹角求点积的公式。f2i易塔云建站-模板下载,web开发资源,技术博客
注：在数学里，向量a和向量b的夹角可记做<a,b>f2i易塔云建站-模板下载,web开发资源,技术博客
这时，有的同学可能会疑惑，为什么这么写就是点积的公式了？这么做有什么意义吗？还是它暗合了图形的某种规律？f2i易塔云建站-模板下载,web开发资源,技术博客
言归正传，为了解开这个谜团，接下来咱们说一下向量的正投影。f2i易塔云建站-模板下载,web开发资源,技术博客
2-向量在轴上的正射投影
我们先分析一下向量的点积公式：f2i易塔云建站-模板下载,web开发资源,技术博客
a·b=|a|*|b|*cosθ
在这里面我们看见了|b|*cosθ，而在三角函数里有这么一个公式：f2i易塔云建站-模板下载,web开发资源,技术博客
cosθ=x/r
x=r*cosθ
对比上面的公式，我们可以猜测：f2i易塔云建站-模板下载,web开发资源,技术博客
- |b|是不是可以作为斜边？
- |b|*cosθ 是不是一条临边？
那咱们画个图看一下：f2i易塔云建站-模板下载,web开发资源,技术博客
f2i易塔云建站-模板下载,web开发资源,技术博客
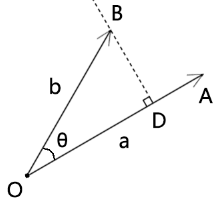
过点B 做OA的垂线BD，则：f2i易塔云建站-模板下载,web开发资源,技术博客
OD=|b|*cosθ
向量OD就叫做向量OB在向量OA上的正射投影。f2i易塔云建站-模板下载,web开发资源,技术博客
因此，点积可以看成向量b在向量a上的正射投影和向量a的长度的乘积。f2i易塔云建站-模板下载,web开发资源,技术博客
接下来，咱们根据上图分析一下点积的性质：f2i易塔云建站-模板下载,web开发资源,技术博客
- 正射投影的值是个实数，可正可负。
- 两个向量的夹角的值域是[0°,180°]
- 两个向量的夹角和点积的关系：
- 当θ=90° 时，b⊥a ，正射投影=0，点积=0
- 当θ=0° 时，b与a同向，正射投影=|b|，点积=|a|*|b|
- 当θ=180° 时，b与a共线，正射投影=-|b|，点积=-|a|*|b|
- 当θ∈[0°,90°) 时，正射投影>0，点积>0
- 当θ∈(90°,180°] 时，正射投影<0，点积<0
- a*b≤|a|*|b|，因为点积可正、可负、可零，|a|*|b|≥0
关于点积的由来我就说到这，接下来咱们说一下点积的运算规律。f2i易塔云建站-模板下载,web开发资源,技术博客
3-点积的运算律
3-1-交换律
a·b=b·a
简单论证一下：f2i易塔云建站-模板下载,web开发资源,技术博客
由向量数量积的定义得：f2i易塔云建站-模板下载,web开发资源,技术博客
a·b=|a|*|b|*cos<a,b>
b·a=|b|*|a|*cos<a,b>
所以：向量的数量积满足交换律f2i易塔云建站-模板下载,web开发资源,技术博客
3-2-分配率
(a+b)·c=a·c+b·c
简单论证一下：f2i易塔云建站-模板下载,web开发资源,技术博客
f2i易塔云建站-模板下载,web开发资源,技术博客
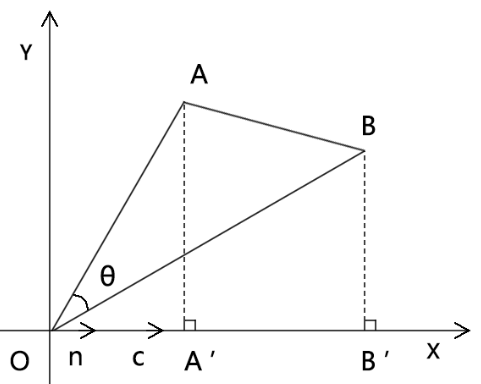
已知：f2i易塔云建站-模板下载,web开发资源,技术博客
- 向量OA
- 向量AB
- 向量OB
- 向量c
- 单位向量n
- 轴向量l
- 轴l、向量n和向量c共线
- 向量a和向量l的夹角为α
- AA'⊥l
- BB'⊥l
求证：f2i易塔云建站-模板下载,web开发资源,技术博客
(OA+AB)·c=OA·c+AB·c
证：f2i易塔云建站-模板下载,web开发资源,技术博客
由向量的点积得：f2i易塔云建站-模板下载,web开发资源,技术博客
AB·n=|OA|*|n|*cosα
因为：向量n是单位向量f2i易塔云建站-模板下载,web开发资源,技术博客
所以：f2i易塔云建站-模板下载,web开发资源,技术博客
|n|=1
所以：f2i易塔云建站-模板下载,web开发资源,技术博客
OA·n=|OA|*|n|*cosα
OA·n=|OA|*1*cosα
OA·n=|OA|*cosα
OA·n=OA'
同理：f2i易塔云建站-模板下载,web开发资源,技术博客
OB·n=OB'
AB·n=A'B'
由向量和角公式可得：f2i易塔云建站-模板下载,web开发资源,技术博客
OB=OA+AB
将OA'、OB'、A'B' 带入其中得：f2i易塔云建站-模板下载,web开发资源,技术博客
(OA+AB)·n=OA·n+AB·n
让等号两边都乘以向量c 的长度|c|，得：f2i易塔云建站-模板下载,web开发资源,技术博客
(OA+AB)·n*|c|=OA·n*|c|+AB·n*|c|
由向量的数乘公式可得：f2i易塔云建站-模板下载,web开发资源,技术博客
c=n*|c|
所以：f2i易塔云建站-模板下载,web开发资源,技术博客
(OA+AB)·n*|c|=OA·n*|c|+AB·n*|c|
(OA+AB)·c=OA·c+AB·c
3-3-其它公式
将向量的交换律和分配率结合起来，还可以推出其它公式。f2i易塔云建站-模板下载,web开发资源,技术博客
(a+b)²=a²+2ab+b²
(a+b)·(a-b)=a²-b²
第二章 基于向量的坐标点求点积f2i易塔云建站-模板下载,web开发资源,技术博客
1-基本公式
已知：f2i易塔云建站-模板下载,web开发资源,技术博客
- 向量a和向量b所在的坐标系为二维直角坐标系
- 向量a的坐标点位是(a1,a2)
- 向量b的坐标点位是(b1,b2)
则向量a和向量b的点积为：f2i易塔云建站-模板下载,web开发资源,技术博客
a·b=a1*b1+a2*b2
上面的公式就是基于向量的坐标点求点积的公式。f2i易塔云建站-模板下载,web开发资源,技术博客
至于这个公式是怎么来的，咱们可以用基于上一章总结出的向量规律论证一下。f2i易塔云建站-模板下载,web开发资源,技术博客
设：二维直角坐标系的正交基底为 {e1(0,1),e2(1,0)}f2i易塔云建站-模板下载,web开发资源,技术博客
则：f2i易塔云建站-模板下载,web开发资源,技术博客
由平面向量基本定理可知：f2i易塔云建站-模板下载,web开发资源,技术博客
a=a1*e1+a2*e2
b=b1*e1+b2*e2
注：f2i易塔云建站-模板下载,web开发资源,技术博客
- a1,a2,b1,b2 都是实数
- e1,e2都是向量
- 实数乘以向量结果还是向量
- 向量和向量相加的结果还是向量
所以：f2i易塔云建站-模板下载,web开发资源,技术博客
a·b=(a1*e1+a2*e2)*(b1*e1+b2*e2)
a·b=a1*b1*e2·e2+a1*b2*e1·e2+a2*b1*e1·e2+a2*b2*e2·e2
由同向向量的点积规律可知：f2i易塔云建站-模板下载,web开发资源,技术博客
e1·e1=|e1|*|e1|=1
e2·e2=|e2|*|e2|=1
由垂直向量的点积规律可知：f2i易塔云建站-模板下载,web开发资源,技术博客
e1·e2=0
e2·e1=0
将上面的四组公式代替a*b的公式，得：f2i易塔云建站-模板下载,web开发资源,技术博客
a·b=a1*b1+a2*b2
上面的证明原理就是现有单位向量将分解坐标点积，然后再利用之前得出的点积规律将单位向量约去。f2i易塔云建站-模板下载,web开发资源,技术博客
关于点积的两个基本公式我就说到这。f2i易塔云建站-模板下载,web开发资源,技术博客
接下来咱们说一个非常重要的知识点，那就是应用。f2i易塔云建站-模板下载,web开发资源,技术博客
因为数学若不学以致用，就会失去前进的动力，要么让人变成书呆子，要么越学越迷茫，反正我是这样感觉的。f2i易塔云建站-模板下载,web开发资源,技术博客
对于如何学以致用，最好是以自己的爱好为驱动。f2i易塔云建站-模板下载,web开发资源,技术博客
数学是本源法，它可以应用于多种领域，比如物理、财经、人工智能、艺术等。f2i易塔云建站-模板下载,web开发资源,技术博客
而我是用艺术来驱动自己对数学的学习的，所以我接下来用点积计算一下物体表面的受光强度。f2i易塔云建站-模板下载,web开发资源,技术博客
f2i易塔云建站-模板下载,web开发资源,技术博客
f2i易塔云建站-模板下载,web开发资源,技术博客
第三章 向量的应用f2i易塔云建站-模板下载,web开发资源,技术博客
f2i易塔云建站-模板下载,web开发资源,技术博客
1-平行光下地面的受光强度
f2i易塔云建站-模板下载,web开发资源,技术博客
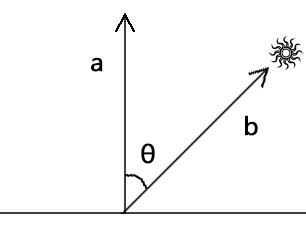
已知：f2i易塔云建站-模板下载,web开发资源,技术博客
- 地面的法线为单位向量a(ax,ay)
- 平行光的方向为单位向量b(bx,by)
求：地面的受光强度cosθf2i易塔云建站-模板下载,web开发资源,技术博客
注：使用单位向量的目的是为了方便运算，我们只关心向量的方向，不关心向量的长度f2i易塔云建站-模板下载,web开发资源,技术博客
解：f2i易塔云建站-模板下载,web开发资源,技术博客
由向量的点积公式可知：f2i易塔云建站-模板下载,web开发资源,技术博客
a·b=|a|*|b|*cosθ
所以：f2i易塔云建站-模板下载,web开发资源,技术博客
cosθ=(a·b)/(|a|*|b|)
根据勾股定理，我们可以求出向量a、b 的长度f2i易塔云建站-模板下载,web开发资源,技术博客
|a|=sqrt(ax*ax+ay*ay)
|b|=sqrt(bx*bx+by*by)
接下来，在求a·b的值即可。f2i易塔云建站-模板下载,web开发资源,技术博客
由向量的点积公式可知：f2i易塔云建站-模板下载,web开发资源,技术博客
a·b=ax*bx+ay*by
所以：f2i易塔云建站-模板下载,web开发资源,技术博客
cosθ=(ax*bx+ay*by)/(sqrt(ax*ax+ay*ay)*sqrt(bx*bx+by*by))
至于为什么我们要用cosθ表示地面的受光强度，我们可以想象一个场景：f2i易塔云建站-模板下载,web开发资源,技术博客
中午的太阳直射地面时：f2i易塔云建站-模板下载,web开发资源,技术博客
θ=0°
地面的受光强度为：f2i易塔云建站-模板下载,web开发资源,技术博客
cosθ=1
这时的光照是最强的。f2i易塔云建站-模板下载,web开发资源,技术博客
黄昏的太阳下山时：f2i易塔云建站-模板下载,web开发资源,技术博客
θ=±90°
地面的受光强度为：f2i易塔云建站-模板下载,web开发资源,技术博客
cosθ=0
这时的光照是最弱的。f2i易塔云建站-模板下载,web开发资源,技术博客
2-图形选择
利用点积可以求两个向量之间的夹角的原理，我们判断一个点是否在三角形中。f2i易塔云建站-模板下载,web开发资源,技术博客
其原理我在另一篇文章里有说，大家可以点击链接进入。f2i易塔云建站-模板下载,web开发资源,技术博客
关于点积的应用，我们就说到这，其实它还有一个兄弟方法，那就是叉乘。f2i易塔云建站-模板下载,web开发资源,技术博客
点积和叉乘的关系，就像余弦与正弦的关系，咱们下一篇详解。f2i易塔云建站-模板下载,web开发资源,技术博客
