第一章 向量在二维坐标系里的姿态
1-平面向量基本定理
平面内任何向量都能用两个不平行向量表示。PG3易塔云建站-模板下载,web开发资源,技术博客
设:PG3易塔云建站-模板下载,web开发资源,技术博客
- 平面内存在一个向量a
- 平面内存在e1、e2 两个不平行的向量
那么:PG3易塔云建站-模板下载,web开发资源,技术博客
- 该平面内存在唯一一对实数a1、a2,使:a=a1e1+a2e2
2-平面向量的特性
在a=a1e1+a2e2 中:PG3易塔云建站-模板下载,web开发资源,技术博客
e1,e2 :二维坐标系里的两个基底,记做{e1,e2}。PG3易塔云建站-模板下载,web开发资源,技术博客
a1e1+a2e2 :向量a关于基底{e1,e2} 的分解式。PG3易塔云建站-模板下载,web开发资源,技术博客
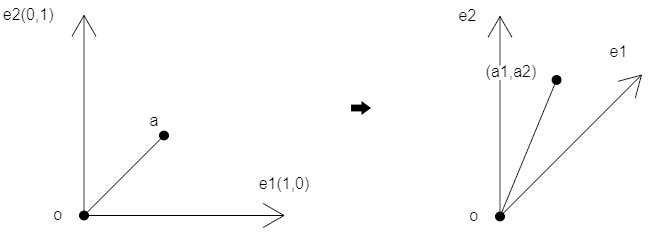
当e1,e2垂直时,如e1(0,1)、e2(1,0) ,其对应的坐标系就是直角坐标系。PG3易塔云建站-模板下载,web开发资源,技术博客
以此原理,我们可以建立两个坐标系的概念。PG3易塔云建站-模板下载,web开发资源,技术博客
-
点a在二维直角坐标系中。PG3易塔云建站-模板下载,web开发资源,技术博客
-
(a1,a2) 可以视之为一个点位,它处于以{e1,e2} 为基底的坐标系中。PG3易塔云建站-模板下载,web开发资源,技术博客
 PG3易塔云建站-模板下载,web开发资源,技术博客
PG3易塔云建站-模板下载,web开发资源,技术博客
我们可以举个例子,加深一下理解。PG3易塔云建站-模板下载,web开发资源,技术博客
3-示例
 PG3易塔云建站-模板下载,web开发资源,技术博客
PG3易塔云建站-模板下载,web开发资源,技术博客
已知:PG3易塔云建站-模板下载,web开发资源,技术博客
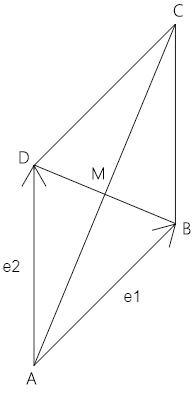
- 平行四边形ABCD
- 向量AB=e1
- 向量AD=e2
求:向量AMPG3易塔云建站-模板下载,web开发资源,技术博客
解:PG3易塔云建站-模板下载,web开发资源,技术博客
AC=AB+AD=e1+e2
DB=AB-AD
AM=AC/2
AM=(e1+e2)/2
AM=e1/2+e2/2
利用向量的基本定理我们还可以推导出一个向量的参数表达式。PG3易塔云建站-模板下载,web开发资源,技术博客
4-向量的参数方程式
向量的参数方程式:PG3易塔云建站-模板下载,web开发资源,技术博客
OP=(1-t)*OA+t*OB
上式中,t 叫做参变量,简称参数。PG3易塔云建站-模板下载,web开发资源,技术博客
由 ① 变换可得:PG3易塔云建站-模板下载,web开发资源,技术博客
OP=OA-t*OA+t*OB
OP=OA+(OB-OA)*t
这个方程式,实际上就是二分法,我们用它可以做缓动跟随。PG3易塔云建站-模板下载,web开发资源,技术博客
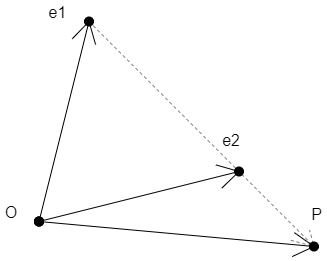
比如,求e1点向e2点移动e1e2长度的t 倍后的点位P,P 就等于 (1-t)OA+tOBPG3易塔云建站-模板下载,web开发资源,技术博客
 PG3易塔云建站-模板下载,web开发资源,技术博客
PG3易塔云建站-模板下载,web开发资源,技术博客
我们可以论证一下上例:PG3易塔云建站-模板下载,web开发资源,技术博客
e1P=t*(e1e2)=t*(e2-e1)
OP=e1+e1P
=e1+t*(e2-e1)
=e1+t*e2-t*e1
=(1-t)*e1+t*e2
向量的参数方程式可以用大白话来解释:点e1向着e2的方向移动,每次移动e1e2距离的t倍。PG3易塔云建站-模板下载,web开发资源,技术博客
PG3易塔云建站-模板下载,web开发资源,技术博客
第二章 向量的正交分解PG3易塔云建站-模板下载,web开发资源,技术博客
PG3易塔云建站-模板下载,web开发资源,技术博客
1-直角坐标系的基本概念
向量垂直:向量所在基线相互垂直,在平面向量基本定理里的直观表现就是e1、e2相互垂直。PG3易塔云建站-模板下载,web开发资源,技术博客
正交基底:e1、e2相互垂直的基底。PG3易塔云建站-模板下载,web开发资源,技术博客
正交分解:在正交基底下分解向量。PG3易塔云建站-模板下载,web开发资源,技术博客
直角坐标的基底的两个分量分别是x轴、y轴上的单位向量{e1,e2},这样的基底也叫做直角坐标系xOy的基底。PG3易塔云建站-模板下载,web开发资源,技术博客
2- 用向量的观点认识直角坐标系
 PG3易塔云建站-模板下载,web开发资源,技术博客
PG3易塔云建站-模板下载,web开发资源,技术博客
在直角坐标系xOy 内,分别取与x、y 方向相同的两个单位向量e1、e2。PG3易塔云建站-模板下载,web开发资源,技术博客
这时,坐标平面内的正交基底就是{e1,e2},这个基底也叫直角坐标系xOy的基底。PG3易塔云建站-模板下载,web开发资源,技术博客
坐标平面xOy 中,作任何一向量a。PG3易塔云建站-模板下载,web开发资源,技术博客
由平面向量基本定理可知,存在唯一有序实数对(a1,a2) 使得:PG3易塔云建站-模板下载,web开发资源,技术博客
a=a1*e1+a2*e2
a1、a2就是向量a 在基底{e1,e2}下的坐标,即:PG3易塔云建站-模板下载,web开发资源,技术博客
a=(a1,a2)
- a1:向量a 在x 轴上的坐标分量
- a2:向量a 在y 轴上的坐标分量
分别通过a 的始点和终点做x、y 轴的垂线,设垂足分别为A1、B1、A2、B2PG3易塔云建站-模板下载,web开发资源,技术博客
- 坐标分量a1 为向量A1B1 在x 轴上的坐标投影
- 坐标分量a2 为向量A2B2 在y 轴上的坐标投影
因为:O 为原点,{e1,e2}为正交基底PG3易塔云建站-模板下载,web开发资源,技术博客
所以O、e1、e2在正交基底{e1,e2} 中的坐标分别为:PG3易塔云建站-模板下载,web开发资源,技术博客
O =(0,0)
e1=(1,0)
e2=(0,1)
设:向量a=(a1,a2),a 的方向相对应x 轴正方向的转角为θPG3易塔云建站-模板下载,web开发资源,技术博客
由三角函数的定义可知:PG3易塔云建站-模板下载,web开发资源,技术博客
a1=|a|*cosθ
a2=|a|*sinθ
3-(x,y)的双重意义
在canvas 画布的坐标系里我们应该知道,其坐标基底{e1,e2} 中:PG3易塔云建站-模板下载,web开发资源,技术博客
至于一个像素的宽高到底是多少毫米,得使用屏幕的物理尺寸去换算,这里我就不再扩展了。PG3易塔云建站-模板下载,web开发资源,技术博客
假如canvas 坐标系里有一点A,点A坐标位是(x,y)PG3易塔云建站-模板下载,web开发资源,技术博客
那么点A的坐标位(x,y)是个什么概念呢?PG3易塔云建站-模板下载,web开发资源,技术博客
我们从坐标原点O 向点A做一个向量OA,则:PG3易塔云建站-模板下载,web开发资源,技术博客
OA=x*e1+y*e2
OA=(x,y)
由上式可知,坐标符号(x,y) 具有两重意义,它可以是一个固定的点(x,y),也可以是向量(x,y)PG3易塔云建站-模板下载,web开发资源,技术博客
我们可以举个例子论证一下:PG3易塔云建站-模板下载,web开发资源,技术博客
已知:PG3易塔云建站-模板下载,web开发资源,技术博客
- e1=(1,0)
- e2=(0,1)
- a1=3
- a2=2
求:aPG3易塔云建站-模板下载,web开发资源,技术博客
解:PG3易塔云建站-模板下载,web开发资源,技术博客
a=3*(1,0)+2*(0,1)
=(3,0)+(0,2)
=(3,2)
接下来咱们说一下向量的坐标运算。PG3易塔云建站-模板下载,web开发资源,技术博客
PG3易塔云建站-模板下载,web开发资源,技术博客
第三章 向量的坐标运算PG3易塔云建站-模板下载,web开发资源,技术博客
PG3易塔云建站-模板下载,web开发资源,技术博客
1-向量运算的基本概念
- 两个向量和与差的坐标等于两个向量相应坐标分量的和与差。
- 向量的数乘等于此数乘以向量的坐标分量。
- 一个向量的坐标等于向量终点的坐标减去向量始点的坐标。
接下来咱们举一个论证两个向量是否共线的例子。PG3易塔云建站-模板下载,web开发资源,技术博客
2-两个向量平行的条件
两个向量平行的条件是:相应坐标成比例PG3易塔云建站-模板下载,web开发资源,技术博客
若a//b (b≠0),则存在唯一实数λ,使a=λbPG3易塔云建站-模板下载,web开发资源,技术博客
逆推,若存在唯一实数λ,使a=λb (b≠0),则a//bPG3易塔云建站-模板下载,web开发资源,技术博客
设:PG3易塔云建站-模板下载,web开发资源,技术博客
- 基底为{e1,e2}
- a=(a1,a2)
- b=(b1,b2)
解:PG3易塔云建站-模板下载,web开发资源,技术博客
a=λb 可分解为:PG3易塔云建站-模板下载,web开发资源,技术博客
(a1,a2)=λ(b1,b2)=(λb1,λb2)
即:PG3易塔云建站-模板下载,web开发资源,技术博客
a1=λb1
a2=λb2



