一，旋转的概念
三维物体的旋转要比位移复杂一点，因为旋转要知道以下几点：

··· 旋转轴
··· 旋转方向
··· 旋转角度

想象一个场景，一个小人站在旋转轴的起点，进行旋转。
小人往左还是往右，就是旋转方向；
小人旋转的大小就是旋转的角度。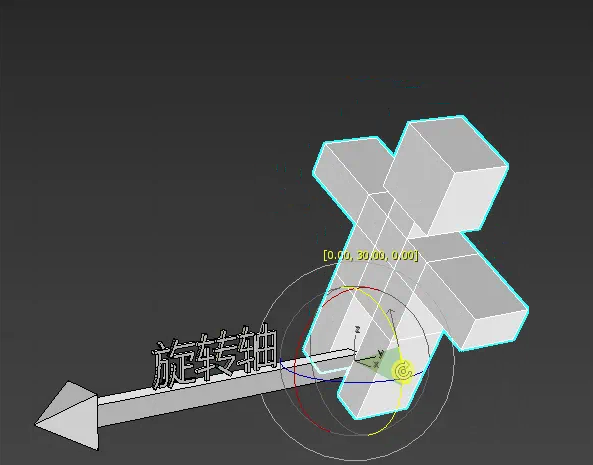



二，旋转方向的正负

何时为正，何时为父。
在WebGL中，除裁剪空间之外的大部分功能都使用了右手坐标系。
我们这里暂且将其视为右手坐标系。



以上图为例
··· 当物体绕z 轴，从x轴正半轴向y轴正半轴逆时针旋转时，是正向旋转，反之为负。
··· 当物体绕x 轴，从y轴正半轴向z轴正半轴逆时针旋转时，是正向旋转，反之为负。
··· 当物体绕y 轴，从z轴正半轴向x轴正半轴逆时针旋转时，是正向旋转，反之为负。

如下图，是正向旋转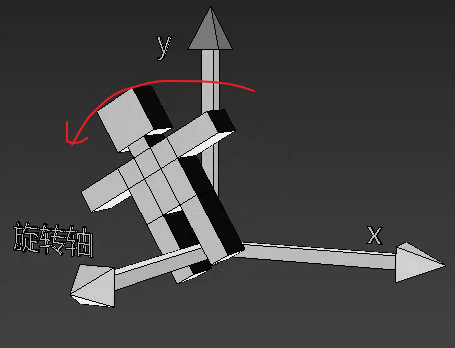



三，旋转公式

先举一个让顶点围绕z 轴旋转的例子。

已知：

··· 点A的位置是(ax,ay,az)
···点A要围绕z轴旋转β度，转到点B的位置

求：点A旋转后的bx、by位置

解：

我们由结果逆推一下解题思路。

因为∠β是已知的，∠α 可以通过点A 得出。

所以我们可以得出：

∠xOB=α+β

那我们通过三角函数就可以推出bx、by

设∠xOB=θ，则：

bx=cosθ*|OA|
by=sinθ*|OA|

上面的|OA|是点O到点A的距离，可以直接用点A求出：

|OA|=Math.sqrt(ax*ax+ay*ay)

那我们接下来只需要知道cosθ和sinθ的值即可

因为：

θ=α+β

所以，我们可以利用和角公式求cosθ和sinθ的值：

cosθ=cos(α+β)
cosθ=cosα*cosβ-sinα*sinβ
sinθ=sin(α+β)
sinθ=cosβ*sinα+sinβ*cosα

所以：

bx=cosθ*|OA|
bx=(cosα*cosβ-sinα*sinβ)*|OA|
bx=cosα*cosβ*|OA|-sinα*sinβ*|OA|
by=sinθ*|OA|
by=(cosβ*sinα+sinβ*cosα)*|OA|
by=cosβ*sinα*|OA|+sinβ*cosα*|OA|

因为：

cosα*|OA|=ax
sinα*|OA|=ay

所以我们可以简化bx、by的公式

bx=ax*cosβ-ay*sinβ
by=ay*cosβ+ax*sinβ

上面的bx、by就是我们要求的答案。