一，原始步骤

考虑一下，为了平移一个三角形，你需要对它的每一个顶点做怎么样的操作？
答案是，你需要对顶点坐标的每个分量（x和y），加上三角形在对应轴（如X轴或Y轴）上平移的距离。
比如，将点 p(x,y,z) 平移到 p'(x',y',z')，在X轴、Y轴、Z轴三个方向上平移的距离分别是 Tx ， Ty，Tz,其中Tz为0。

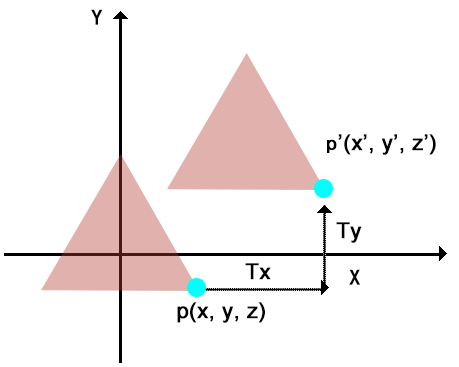
x' = x + Tx
y' = y + Ty
z' = z + Tz

我们只需要在着色器中为顶点坐标的每个分量加上一个常量就可以实现上面的灯饰。
显然，这是一个逐顶点的操作，而非逐片元，上述修改应该发生在顶点着色器。
顶点着色器中： gl_Position = a_Position + u_Translation;\n
js中：var Tx = 0.5, Ty = 0.5, Tz = 0.0;
传递给着色器：
1. var u_Translation = gl.getUniformLocation(gl.program, 'u_Translation');
2. gl.uniform4f(u_Translation, Tx, Ty, Tz, 0.0);

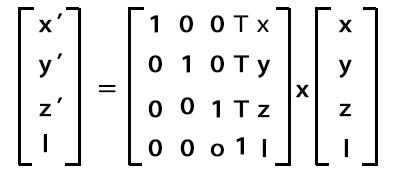
二，平移矩阵

首先理解一下，矩阵和矢量的相乘。如果将一个点p的坐标，变换为点p'，可以通过矩阵来进行变换。即：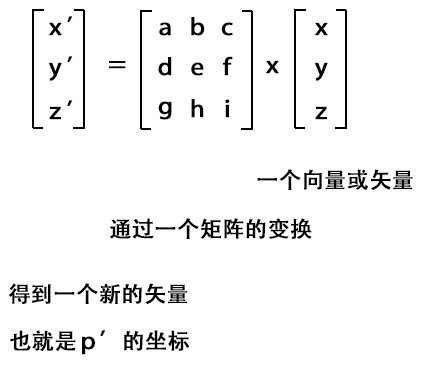

等式：
ｘ＇　＝　ａｘ　＋　ｂｙ　＋　ｃｚ
ｙ＇　＝　ｄｘ　＋　ｅｙ　＋　ｆｚ
ｚ＇　＝　ｇｘ　＋　ｈｙ　＋　ｉｚ

我们比较：
ｘ＇　＝　ａｘ　＋　ｂｙ　＋　ｃｚ　．．．
ｘ＇　＝　ｘ　＋　Ｔｘ
因为等式二有常量Ｔｘ，所以我们引入４维矩阵，有
ｘ＇　＝　ａｘ　＋　ｂｙ　＋　ｃｚ　＋　ｄ
ｙ＇　＝　ｅｘ　＋　ｆｙ　＋　ｇｚ　＋　ｈ
ｚ＇　＝　ｉｘ　＋　ｊｙ　＋　ｋｚ　＋　ｌ
ｌ　　＝　ｍｘ　＋　ｎｙ　＋　ｏｚ　＋　ｐ
比较：
x' = x + Tx
y' = y + Ty
z' = z + Tz
比较ｘ＇，ａ＝１，ｂ＝ｃ＝０，ｄ＝Ｔｘ
比较ｙ＇，ｅ＝ｇ＝０，ｆ＝１，ｈ＝Ｔｙ
比较ｚ＇，ｉ＝ｊ＝０，ｋ＝１，ｌ＝Ｔｚ
最后一行，容易得到，ｍ＝ｎ＝ｏ＝０，ｐ＝ｌ
这样，写出平移矩阵：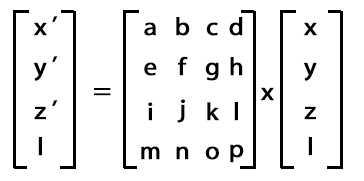

则：