一，原始步骤

旋转比平移复杂一些，因为描述一个旋转本身就比描述一个平移复杂。为了描述旋转，你应该知道：
1. 旋转轴（图形将围绕旋转轴旋转）
2. 旋转方向（方向：顺时针或逆时针）
3. 旋转角度（图形旋转经过的角度）
这里这样描述：绕Z轴，逆时针旋转了 β 角度。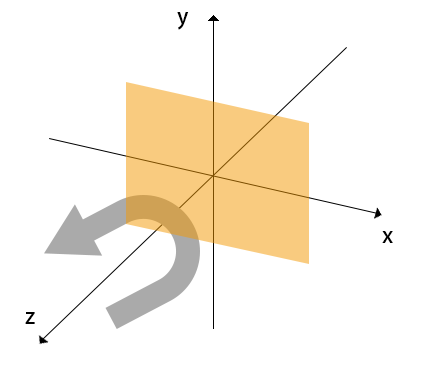

右手旋转法则：右手握拳，大拇指伸直并使其指向旋转轴的正方向，那么右手其余几个手指就指明了旋转的方向。现在我们看下旋转的数学表达式：
设点p(x, y, z)旋转 β 角度之后变为 p'(x', y', z') ；首先旋转是绕z轴进行的，所以z坐标不会变，直接忽略，然后，x轴和y轴的情况有一些复杂。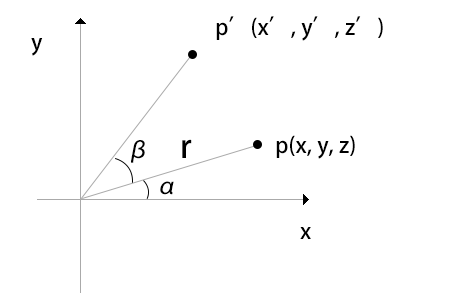

由于：
x = r cos α
y = r sin α
类似的，你也可以表示点p'的坐标
x' = r cos (α + β)
y' = r sin (α + β)
利用三角函数可得
x' = r (cos α cos β - sin α sin β)
y' = r (sin α cos β + cos α sin β)
将等式1代入上式，得
x' = x cos β - y sin β
y' = y cos β + x sin β
z' = z
现在我们就可以把sin β 和 cos β 通过js 传递给着色器。
着色器：
gl_Position.x = a_Position.x * u_CosB - a_Position.y * u_SinB;
gl_Position.y = a_Position.x * u_SinB + a_Position.y * u_CosB;
js：
var u_CosB = gl.getUniformLocation(gl.program, "u_CosB");
var u_SinB = gl.getUniformLocation(gl.program, "u_SinB");
gl.uniform1f(u_CosB );
gl.uniform1f(u_SinB );

二，旋转矩阵

由上一篇的平移矩阵，我们同样可以推理出，旋转矩阵，如图：

三，沿X轴旋转和Y轴旋转的推到过程：